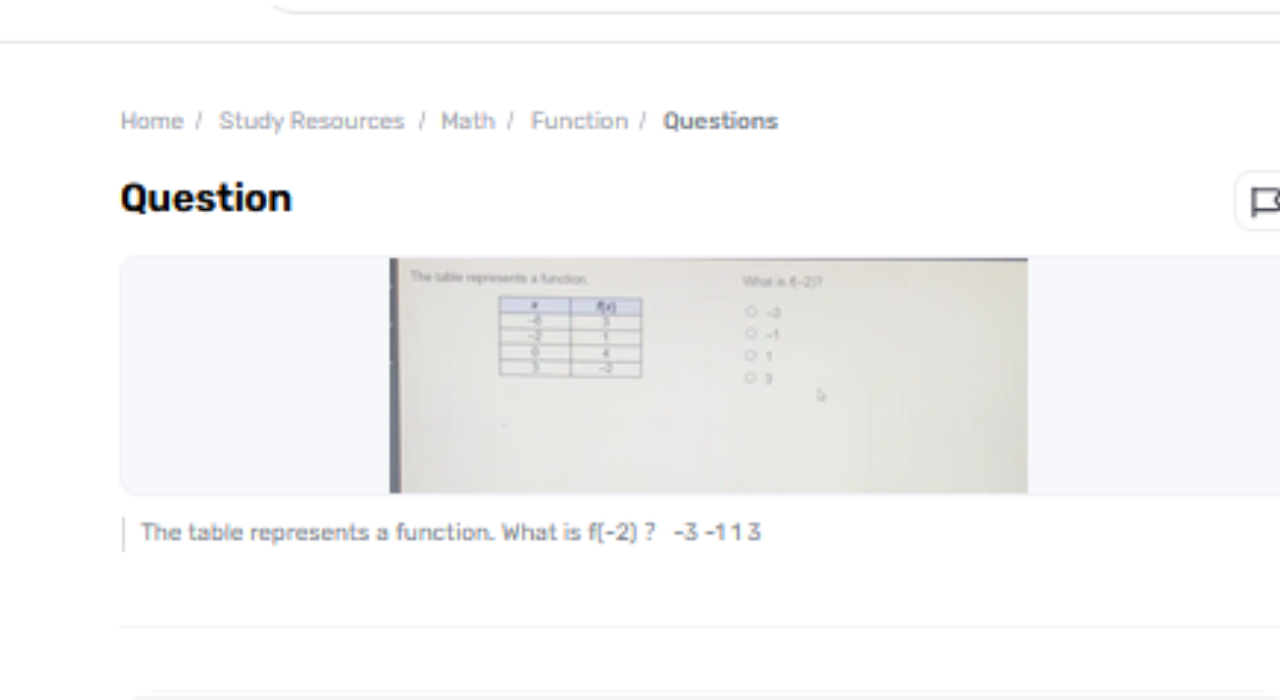
Capacities are principal concepts in science, speaking to connections between sets of values. To decide the yield of work for a given input, we frequently allude to a table that traces these connections. In this article, we'll address how to discover the esteem of f(-2)f(-2)f(-2) from a table speaking to a work. By understanding the structure of such tables and how they pass on work values, able to precisely decide the function's yield for the desired input.
Nitty Gritty Steps for Tackling the Condition 24+10z=3124 + 10z = 3124+10z=31
In variable-based math, tackling conditions like 24+10z=31 is crucial for understanding variable connections the table represents a function. what is f(–2)? –3 –1 1 3 This illustration outlines how to confine the variable zzz through an arrangement of arithmetical operations. We are going to carefully break down each step, from disentangling the condition to fathoming for zzz, and verify the solution to guarantee exactness. This preparation highlights the systematic approach required to fathom direct conditions successfully.
Identifying the Right Yield Esteem
Given the choices for f(-2)f(-2)f(-2): -3, -1, 1, or 3, we must coordinate these choices with the proper yield from the table. To unravel this, we look at the table and explore the push where the input is -2. The yield esteem in this row represents f(-2)f(-2)f(-2). If the table isn't given expressly, we depend on the data given or setting clues. For occurrence, on the off chance that we have been told that f(-2)f(-2)f(-2) is one of the four given choices, the right esteem must coordinate one of these choices. By assessing the setting or any extra data given, ready to distinguish the proper yield esteem.
Confirming the Functions Yield
To guarantee exactness, it is imperative to confirm that the chosen yield esteem accurately corresponds to the input of -2. We will cross-check by confirming that the work table or run the show bolsters this esteem. On the off chance that the table is exact and total, the distinguished esteem for f(-2)f(-2)f(-2) ought to consistently fit the functions mapping. Any errors or irregularities ought to be looked into to affirm the rightness of the yield esteem.
Primary Steps for Utilizing Gauth to Total Homework
Yield Your Request
Start by entering your particular homework address into Gauth. You'll sort it out or transfer significant records. Guarantee your input is nitty gritty and exact to get the foremost exact help. Gauth will assess your accommodation to supply the leading conceivable back.
Audit the Answers and Clarifications
Once Gauth forms your inquiry, carefully audit the step-by-step solutions and clarifications given. This makes a difference you get a handle on the strategies and ideas utilized to solve the issue. Understanding these subtle elements will prepare you to handle comparative issues successfully in the future.
Hone and Evaluate Your Information
Take advantage of Gauth's intelligently highlights, like tests and additional hone issues, to test and upgrade your understanding of the fabric. Utilize these apparatuses to set your information. On the off chance that you confront challenges, return to Gauth’s clarifications and assets to guarantee exhaustive comprehension sometime after recently completing your homework.
Conclusion
In conclusion, deciding the esteem of f(-2)f(-2)f(-2) from a work table includes finding the required input within the table and distinguishing the comparing yield esteem. Given the alternatives -3, -1, 1, and 3, the rectified esteem of f(-2)f(-2)f(-2) can be found by counseling the table and coordinating the input with its yield. Precise translation of work tables and understanding their structure are basic for tackling such issues. By taking these steps, one can viably decide the esteem of a work for any given input.